Autor: João Victor Assaoka Ribeiro
Ao desenvolver modelos de regressão, a avaliação de desempenho é fundamental para entender o quão bem o modelo está prevendo os resultados. Para isso, usamos diferentes métricas de erro, que nos ajudam a medir a qualidade das previsões em relação aos valores reais. Aqui estão algumas das métricas mais utilizadas:
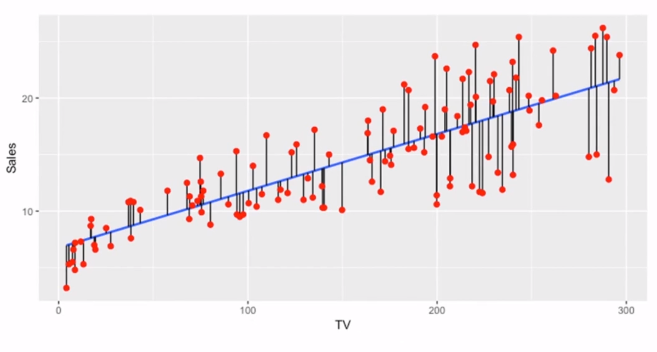
Erro Quadrático Médio (MSE)
O Erro Quadrático Médio (MSE) é uma das métricas mais comuns para avaliar modelos de regressão. Ele calcula a média dos quadrados das diferenças entre os valores reais e os valores previstos. O fato de ele elevar os erros ao quadrado faz com que erros maiores tenham um impacto muito maior na métrica. Isso significa que o MSE penaliza mais os erros grandes, tornando-o útil quando queremos garantir que o modelo minimize grandes desvios.
Vantagem:
Penaliza grandes erros de forma mais severa.
Desvantagens:
Sensível a outliers, o que pode distorcer a avaliação se houver valores muito discrepantes nos dados.
A unidade do MSE é diferente da variável alvo, dificultando a interpretação direta.
Variação: Raiz do Erro Quadrático Médio (RMSE)
O RMSE é a raiz quadrada do MSE. Ele resolve o problema da unidade, trazendo-a de volta ao mesmo nível da variável alvo, tornando a métrica mais interpretável. Além disso, o RMSE ainda mantém a característica de penalizar erros maiores, o que é vantajoso em muitos cenários.
O RMSE é muito útil em casos como a previsão de vida útil restante de uma máquina, onde queremos penalizar previsões muito distantes do valor real. Como ele traz a métrica para a mesma unidade da variável de interesse, facilita a interpretação dos resultados.
Erro Absoluto Médio (MAE)
O Erro Absoluto Médio (MAE) mede a média dos valores absolutos das diferenças entre as previsões e os valores reais. Ao contrário do RMSE, o MAE não penaliza de forma tão severa os grandes erros, sendo assim menos sensível a outliers. Isso o torna uma métrica interessante quando queremos dar igual importância a todos os erros, independentemente de seu tamanho.
Vantagem:
Menos sensível a outliers
Variação: Erro Percentual Absoluto Médio (MAPE)
O MAPE calcula o erro como uma porcentagem em relação ao valor real. Ele é útil quando a proporção do erro é mais importante do que o valor absoluto do erro. Por exemplo, um erro de 10 em uma previsão de 100 é mais relevante do que um erro de 10 em uma previsão de 1000.
Coeficiente de Determinação (R²)
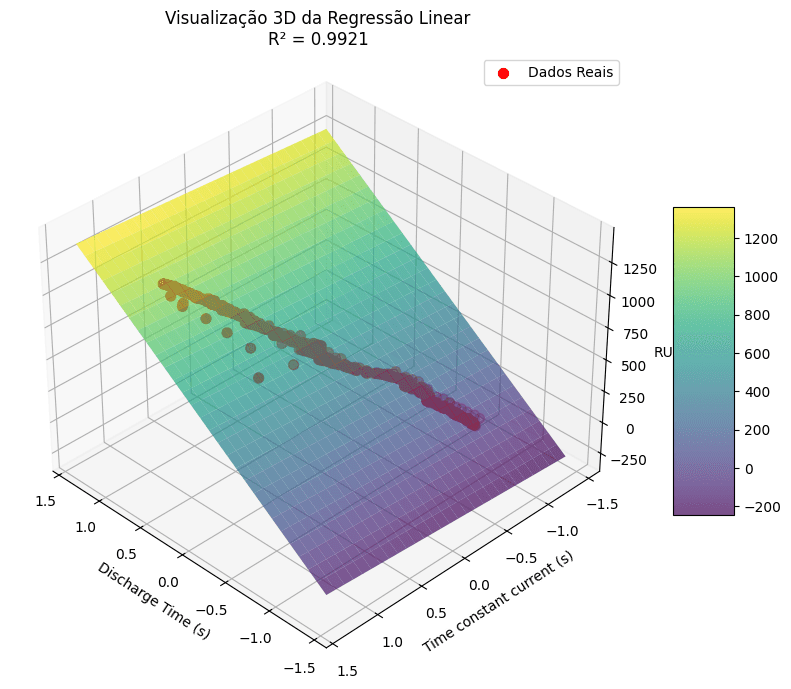
O Coeficiente de Determinação (R²) mede a proporção da variância da variável alvo que é explicada pelo modelo. Ele avalia o quão bem o modelo se ajusta aos dados e varia entre 0 e 1, sendo que 1 indica um ajuste "perfeito". O R² é uma métrica relativa, ou seja, ele compara o modelo com um modelo base que apenas retorna a média dos valores reais como previsão.
Um R² próximo de 1 significa que o modelo explica bem a variação dos dados, enquanto um valor próximo de 0 indica que o modelo tem um desempenho ruim. Um R² negativo sugere que o modelo é pior do que simplesmente prever a média.