Autor: João Victor Assaoka Ribeiro
A importância por permutação (Permutation Importance) é uma técnica poderosa e intuitiva para identificar as variáveis mais relevantes em previsões de modelos de machine learning. Diferente de muitas outras abordagens de interpretabilidade, essa técnica é simples de implementar manualmente, permitindo adaptações específicas para diferentes algoritmos e aplicações.
Intuição do Funcionamento
Imagine que você possui um modelo para prever o momento de falha de uma máquina e várias informações disponíveis, como temperatura, vibração, idade do equipamento, pressão do óleo, entre outras. A pergunta que surge é: qual dessas informações é a mais importante para uma previsão precisa?
A importância por permutação traz uma abordagem simples e genial:
Primeiro, medimos o desempenho do modelo com os dados originais.
Em seguida, "embaralhamos" uma variável aleatoriamente e medimos o desempenho novamente n vezes.
Repetimos isso para cada variável e comparamos o desempenho original com o desempenho permutado.
A lógica é que, se embaralharmos uma variável importante, o desempenho do modelo deve cair significativamente. Por outro lado, se a variável não for tão relevante, o impacto será pequeno, ou quase inexistente. Em casos raros, o desempenho pode até melhorar, indicando que a variável talvez estivesse atrapalhando as previsões.
É como se "vendássemos" o modelo em relação a uma informação específica e observássemos o impacto nas previsões. Dessa forma, conseguimos medir, de maneira prática, a importância de cada variável.
Implementação em Python
Passo 1: Preparação do Ambiente e Dados
# Instalando as bibliotecas necessárias
!pip install pandas numpy scikit-learn matplotlib xgboost
# Importando as bibliotecas necessárias
import pandas as pd
import numpy as np
import xgboost as xgb
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error, mean_absolute_error, r2_score
import matplotlib.pyplot as pltPasso 2: Preparação dos Dados e Treinamento do Modelo
# Carregar os dados
arquivo = '/content/drive/MyDrive/Datasets Públicos/Battery_RUL.csv' # Endereço do arquivo .csv
df = pd.read_csv(arquivo)
# Separar features e target
X = df.drop('RUL', axis=1)
y = df['RUL']
# Dividir em treino e teste
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Criar e treinar um modelo (vamos usar XGBoost como exemplo)
model = xgb.XGBRegressor(n_estimators=500, random_state=42)
model.fit(X_train, y_train)Passo 3: Implementação da Função de Importância por Permutação (Versão Simples)
Podemos implementar uma função básica para calcular a importância por permutação com base no erro médio absoluto (MAE) da seguinte forma:
def permutation_importance (modelo, x, y, n_perm):
# Calcula as métricas de referência
previsão = modelo.predict(x)
MAE = mean_absolute_error(y, previsão)
print(f'''Valor de referência:\n - MAE: {MAE:.2f}\n''')
# Para cada cluster de colunas, calcula a importância da permutação
importance = []
for feature_name in x.columns:
pontuações_MAE = []
for i in range(n_perm):
x_perm = x.copy()
np.random.seed(i)
# Gerar uma permutação aleatória
idx_permutacao = np.random.permutation(len(x_perm))
x_perm[feature_name] = x_perm[feature_name].values[idx_permutacao]
# Fazer previsões com os dados permutados
previsão_perm = modelo.predict(x_perm)
pontuações_MAE.append(mean_absolute_error(y, previsão_perm) - MAE)
importance.append({
'Atributo': feature_name,
'Importância': np.mean(pontuações_MAE)
})
# Retorna a importância da permutação ordenada
return pd.DataFrame(importance).sort_values(by='Importância', ascending=False)# Calcular importância
importancia_perm = permutation_importance(model, X_test, y_test, n_perm=10)
importancia_perm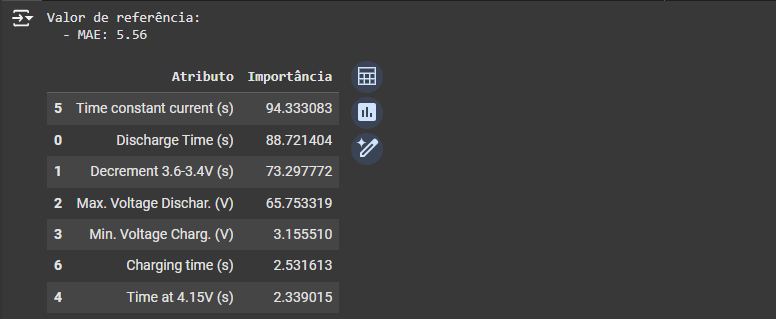
Passo 3: Visualização dos Resultados de Forma Gráfica
def plot_importances(importances, metric='Importância', title=None):
plt.figure(figsize=(10, 6))
plt.bar(importances['Atributo'], importances[metric])
plt.xticks(rotation=45, ha='right')
plt.title(title or f'Importância das Features por Permutação ({metric})')
plt.xlabel('Feature/Cluster')
plt.ylabel(f'Aumento em {metric}')
plt.tight_layout()
plt.show()
# Plotar importâncias individuais
plot_importances(importancia_perm, metric='Importância', title='Importância por Permutação')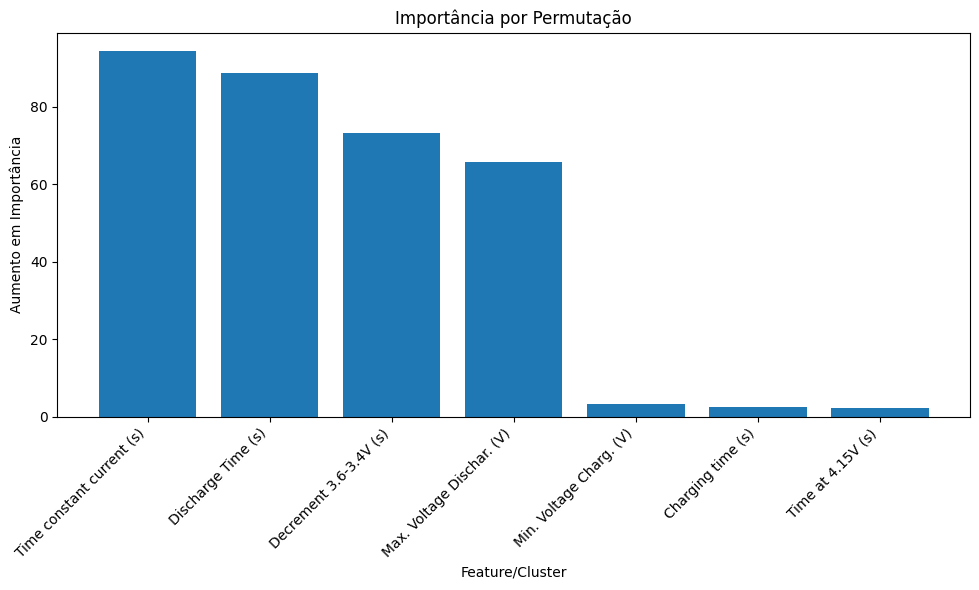
Interpretando os Resultados
Ao analisar os resultados, podemos tirar várias conclusões importantes:
Features com maior importância: São aquelas que, ao serem embaralhadas, causam uma queda significativa no desempenho do modelo. São as variáveis que mais impactam o desempenho e, portanto, são cruciais para monitoramento.
Features com baixa importância: Ao serem embaralhadas, quase não afetam o modelo, indicando que podem ser transformadas ou até descartadas em otimizações futuras.
Implementação Aprimorada:
Podemos fazer algumas alterações para fazer uma análise mais robusta, como:
Métricas Diversas: Podemos incluir outras métricas, como RMSE e R2, para obter uma visão mais detalhada do impacto da permutação.
Agrupamento de Features: Podemos agrupar variáveis relacionadas em "clusters" e calcular a importância do grupo. Isso é especialmente útil quando falamos de manutenção preditiva, onde uma das estratégias mais famosas para capturar tendências é a criação de lags (atrasos) das variáveis preditoras.
Controle de Diferença de Métricas: Permitindo que o usuário escolha se deseja a diferença entre a métrica original e a permutada ou apenas a métrica permutada. Isso pode ser útil principalmente para métricas como R2, onde valores negativos são possíveis (modelos piores que a média).
def permutation_importance (modelo, x, y, n_perm, feature_clusters = None, diff = True):
# Calcula as métricas de referência
previsão = modelo.predict(x)
RMSE = root_mean_squared_error(y, previsão)
MAE = mean_absolute_error(y, previsão)
R2 = r2_score(y, previsão)
print(f'''Valor de referência:\n - RMSE: {RMSE:.2f}\n - MAE: {MAE:.2f}\n - R2: {R2:.2f}''')
# Se não houver clusters definidos, trata cada coluna independentemente
if feature_clusters is None:
features_to_permute = {col: [col] for col in x.columns}
else:
features_to_permute = feature_clusters
# Para cada cluster de colunas, calcula a importância da permutação
importance = []
for feature_name, feature_cols in features_to_permute.items():
pontuações_RMSE = []
pontuações_MAE = []
pontuações_R2 = []
for i in range(n_perm):
x_perm = x.copy()
np.random.seed(i)
# Gera uma permutação única para todas as colunas do cluster
idx_permutacao = np.random.permutation(len(x_perm))
for col in feature_cols:
x_perm[col] = x_perm[col].values[idx_permutacao]
# Fazer previsões com os dados permutados
previsão_perm = modelo.predict(x_perm)
pontuações_RMSE.append((root_mean_squared_error(y, previsão_perm) - (RMSE if diff else 0)))
pontuações_MAE.append((mean_absolute_error(y, previsão_perm) - (MAE if diff else 0)))
pontuações_R2.append((r2_score(y, previsão_perm) - (R2 if diff else 0)))
importance.append({
'Atributo': feature_name,
'Média_RMSE': np.mean(pontuações_RMSE),
'Média_MAE': np.mean(pontuações_MAE),
'Média_R2': np.mean(pontuações_R2)
})
# Se clusters foram definidos, adiciona a lista de atributos que compõem o cluster
if feature_clusters is not None:
importance[-1]['Atributos'] = feature_cols
# Retorna a importância da permutação ordenada
return pd.DataFrame(importance).sort_values(by='Média_RMSE', ascending=False)clusters = {
'Tempo de Descarga e Carregamento': ['Discharge Time (s)', 'Charging time (s)', 'Time constant current (s)'],
'Tensões de Descarga e Carregamento': ['Max. Voltage Dischar. (V)', 'Min. Voltage Charg. (V)', 'Decrement 3.6-3.4V (s)'],
'Tempo em Tensões Específicas': ['Time at 4.15V (s)']
}
permutation_importance(model, X_test, y_test, n_perm=10, feature_clusters=clusters, diff=False)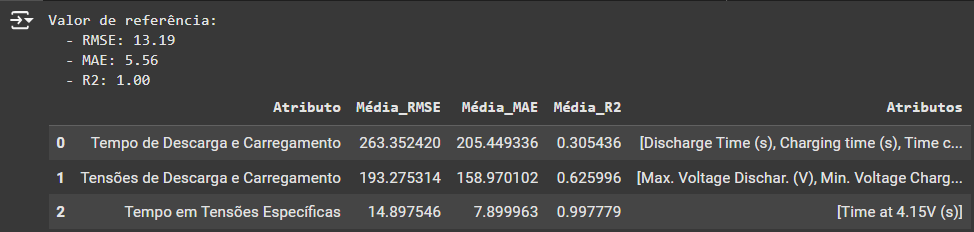
Conclusão
A importância por permutação é uma técnica valiosa para entender quais variáveis são mais relevantes em seu modelo de manutenção preditiva. Sua simplicidade conceitual e implementação direta a tornam uma excelente escolha para começar a explorar a interpretabilidade, mesmo em modelos de "caixa preta".
Lembre-se que esta é apenas uma das várias técnicas disponíveis para interpretabilidade de modelos. Em situações reais, é recomendável usar múltiplas técnicas para ter uma visão mais completa do seu modelo.
Você pode experimentar este código no Google Colab. Faça uma cópia do notebook e adapte-o para seus próprios dados e necessidades. Como sujestão de experimentos, você pode:
Teste diferentes números de repetições (Quanto mais repetições, mais confiável será a importância)
Testar diferentes clusters de features (na prática, você pode ter features relacionadas que fazem mais sentido serem agrupadas)
Experimente diferentes métricas de erro
Se tiver alguma dúvida, você pode entrar em contato comigo.