Autor: João Victor Assaoka Ribeiro

A regressão linear é um algoritmo essencial em aprendizado de máquina, especialmente útil para problemas de previsão de valores numéricos contínuos.

A técnica consiste em encontrar uma reta (ou hiperplano) que melhor se ajuste aos dados, minimizando a diferença entre os valores reais e os previstos. Ela é representada pela equação:

y = β₀ + β₁x₁ + β₂x₂ + ... + βₙxₙ + ε

Onde:

- y é a variável dependente (valor a ser previsto)

- β₀ é o coeficiente linear (também chamado de intercepto ou viés)

- βᵢ são os coeficientes lineares das variáveis independentes xᵢ

- ε é o erro

Vantagens e Desvantagens da Regressão Linear

Entre as principais vantagens da regressão linear, destacam-se:

1. Interpretabilidade: Os coeficientes do modelo representam a contribuição linear de cada variável preditora para a variável de saída, permitindo uma análise clara das relações entre as variáveis.

2. Simplicidade e Eficiência Computacional: Os algoritmos de regressão linear são simples de implementar e computacionalmente eficientes.

Apesar de suas vantagens, a regressão linear também apresenta algumas limitações:

1. Assunção de Linearidade: A regressão linear assume que a relação entre as variáveis é aproximadamente linear. Se a relação for não linear, o modelo pode não se ajustar bem aos dados.

2. Sensibilidade a Outliers: Por tentar minimizar a soma dos erros quadrados, a regressão linear é sensível a outliers, que podem distorcer significativamente o modelo.

Implementando Regressão Linear em Python

Neste exemplo, vamos usar uma base de dados em formato .csv, que contém informações sobre uma bateria. Nosso objetivo é prever a vida útil restante da bateria com base nas variáveis disponíveis. Esse dataset pode ser encontrado no kaggle. Tratamos esse conjunto de dados selecionando apenas a primeira bateria e excluindo a característica Cycle_Index para simplificar o exemplo. Você pode baixar o arquivo aqui.

Passo 1: Preparação do Ambiente

# Instalando as bibliotecas necessárias
!pip install pandas numpy scikit-learn matplotlib

# Importando as bibliotecas necessárias
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import RobustScaler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

Passo 2: Preparação dos Dados

# Carregar os dados
arquivo = '/content/drive/MyDrive/Datasets Públicos/Battery_RUL.csv' # Endereço do arquivo .csv
df = pd.read_csv(arquivo)

# Separar features e target
X = df.drop('RUL', axis=1)
y = df['RUL']

# Dividir em treino e teste
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Ordenando os dataframes
X_train = X_train.sort_index()
y_train = y_train.sort_index()
X_test = X_test.sort_index()
y_test = y_test.sort_index()

# Normalizar os dados
def Normalizar_RobustScaler(df):
    scaler = RobustScaler()
    df_scaled = pd.DataFrame(scaler.fit_transform(df), columns=df.columns, index=df.index)
    return df_scaled, scaler

X_train_norm, scaler = Normalizar_RobustScaler(X_train)
X_test_norm = pd.DataFrame(scaler.transform(X_test), columns=X_test.columns, index=X_test.index)

Passo 3: Treinamento do Modelo

# Criar e treinar um modelo de regressão linear
modelo = LinearRegression()
modelo.fit(X_train_norm, y_train)

Passo 4: Avaliação do Modelo

# Fazer previsões
y_pred = modelo.predict(X_test_norm)

# Calcular o coeficiente de determinação (R²)
r2 = modelo.score(X_test_norm, y_test)
print(f"Coeficiente de Determinação (R²): {r2:.4f}")

# Visualizando as previsões
plt.figure(figsize=(10, 6))
plt.plot(y_test.values, label='Real')
plt.plot(y_pred, label='Previsto')
plt.title(f'Real vs. Previsto - R2: {r2:.4f}')
plt.legend(loc='upper right')
plt.show()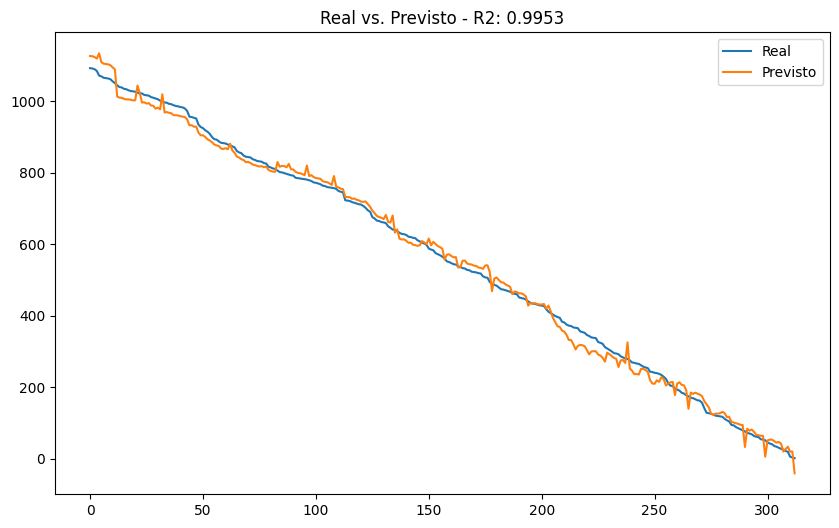

Passo 5: Extração dos Coeficientes

# Extrair os coeficientes do modelo
coeficientes = pd.DataFrame(modelo.coef_, 
                            index=X.columns, 
                            columns=['Coeficiente'])
coeficientes.loc['Intercepto'] = modelo.intercept_
print(coeficientes)

A normalização dos dados é crucial para garantir que todas as variáveis estejam na mesma escala, facilitando tanto a convergência do modelo quanto a interpretação dos coeficientes. Sem essa normalização, alguns coeficientes podem acabar "compensando" as diferenças de escala entre as variáveis, o que pode dificultar a interpretação dos resultados.

Os coeficientes permitem comparar diretamente a importância relativa de cada variável no modelo. Por exemplo, se o valor absoluto do coeficiente de 'Discharge Time' for maior do que o de 'Time constant current', podemos concluir que 'Discharge Time' tem um impacto maior na previsão da vida útil restante (RUL).

Intuição por Trás da Regressão Linear

Vamos considerar uma versão simplificada do nosso problema, onde temos apenas duas variáveis preditoras: 'Discharge Time' e 'Time constant current'. Nesse cenário, a regressão linear pode ser representada graficamente como um plano em um espaço tridimensional, onde as variáveis preditoras correspondem aos eixos x e y, e a variável de saída (RUL) corresponde ao eixo z.

Visualizar esse plano de regressão linear ajustado aos dados nos permite entender melhor como o modelo faz previsões com base nas variáveis de entrada.

def visualizar_regressao_3d(modelo, x, y, scaler, feature_names=['Feature 1', 'Feature 2']):
    # Criar malha de pontos para o plano
    x_min, x_max = x.iloc[:, 0].min() - 0.5, x.iloc[:, 0].max() + 0.5
    y_min, y_max = x.iloc[:, 1].min() - 0.5, x.iloc[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
                        np.arange(y_min, y_max, 0.1))
    
    # Fazer predições para todos os pontos da malha
    Z = modelo.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    # Criar figura 3D
    fig = plt.figure(figsize=(12, 8))
    ax = fig.add_subplot(111, projection='3d')
    
    # Plotar o plano de predição com menor transparência
    surf = ax.plot_surface(xx, yy, Z, alpha=0.7, cmap='viridis')
    
    # Plotar os pontos reais
    scatter = ax.scatter(x.iloc[:, 0], x.iloc[:, 1], y,
                        c='red', marker='o', s=50, label='Dados Reais')
    
    # Adicionar barra de cores
    fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)
    
    # Configurar rótulos dos eixos
    ax.set_xlabel(feature_names[0])
    ax.set_ylabel(feature_names[1])
    ax.set_zlabel('RUL')
    
    # Adicionar título e legenda
    ax.set_title('Visualização 3D da Regressão Linear\nR² = {:.4f}'.format(modelo.score(x, y)))
    ax.legend()

    # Ajustar ângulo de visualização para melhor perspectiva
    ax.view_init(elev=35, azim=135)
    plt.show()
    return fig, ax

# Simplificar os dados
cols = ['Discharge Time (s)', 'Time constant current (s)']
X_simplificado = X_train[cols]
X_simplificado, scaler_simplificado = Normalizar_RobustScaler(X_simplificado)

# Treinar um modelo simplificado
modelo_simplificado = LinearRegression()
modelo_simplificado.fit(X_simplificado, y_train)

# Visualizar o plano de regressão 3D
visualizar_regressao_3d(modelo_simplificado, X_simplificado, y_train, scaler_simplificado, feature_names=cols)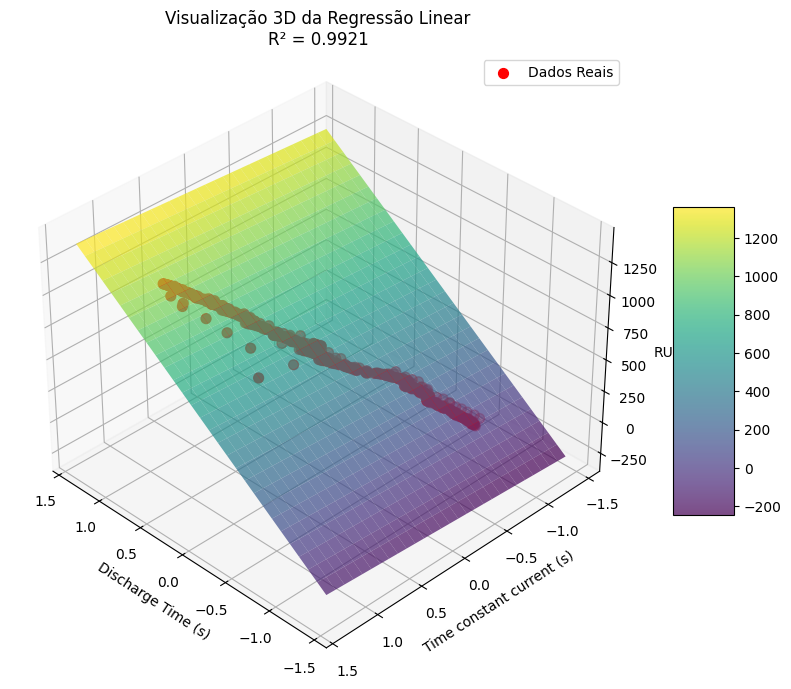

Nesta visualização 3D, podemos ver o plano de regressão linear ajustado aos dados. Os coeficientes do modelo determinam a inclinação desse plano em relação a cada variável de entrada, permitindo uma interpretação clara da contribuição de cada feature.

Conclusão

Neste post, apresentamos os conceitos básicos da regressão linear e mostramos como implementá-la em Python usando a biblioteca Scikit-learn. A regressão linear é um modelo simples que se destaca pela alta interpretabilidade dos coeficientes, simplicidade de implementação e eficiência computacional.

Você pode experimentar esse código no Google Colab. Faça uma cópia do notebook e adapte-o para seus próprios dados e necessidades. Se tiver alguma dúvida, você pode consultar a documentação oficial do Scikit-learn para obter mais informações ou entrar em contato comigo.

Powered by wisp