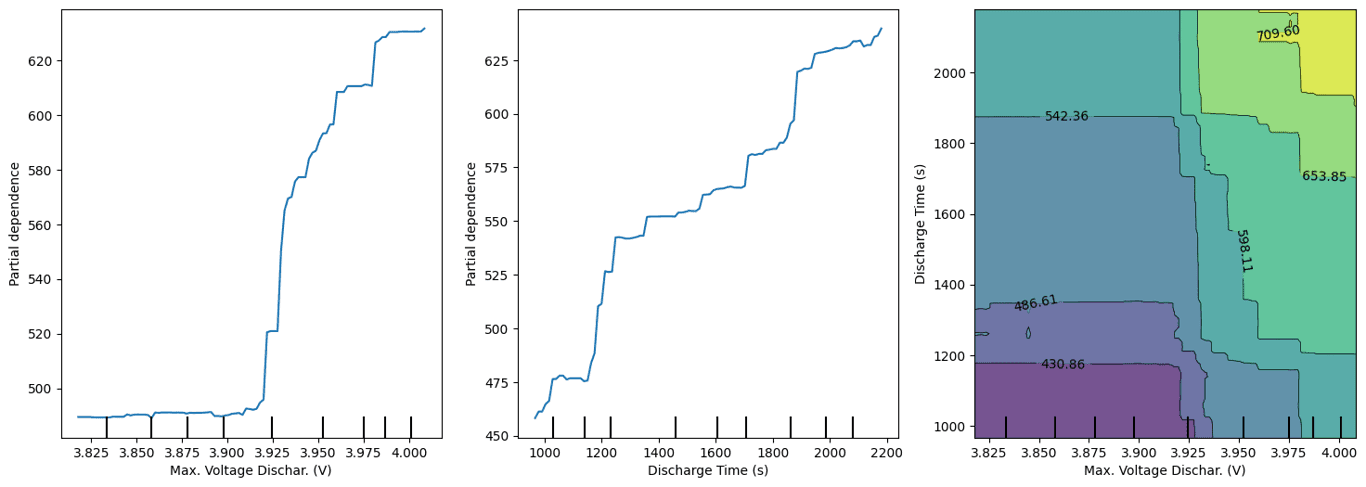
Os Accumulated Local Effects (ALE) são uma técnica de interpretabilidade de modelos de machine learning que serve como alternativa aos Partial Dependence Plots (PDPs). Assim como os PDPs, os ALEs visam compreender como uma característica individual afeta a previsão de um modelo, mantendo as outras características constantes.
A principal motivação para o uso de ALE plots é que os PDPs podem fornecer estimativas viesadas dos efeitos das variáveis quando elas são correlacionadas. Isso ocorre porque os PDPs calculam a média das previsões do modelo ao fixar uma variável em certos valores, ignorando a distribuição condicional das outras variáveis. Isso pode levar a combinações irrealistas de valores das variáveis, afetando a interpretação dos resultados.
A principal diferença é que os ALEs são mais robustos a interações entre características e a outliers, além de serem computacionalmente mais eficientes.
Intuição por trás dos ALEs
Para facilitar a visualização do problema apresentado acima, vamos supor que queremos prever a altura que alguém pode pular de acordo com sua altura e peso.
Na hora de gerar um Gráfico de Dependência Parcial (PDP) da altura, esse método iria escolher um valor fixo de peso e forçar todas as instâncias a terem esse valor, para então calcular a média das previsões do modelo. Isso pode gerar pontos que não fazem sentido, como alguém de 2 metros de altura pesando 30 kg, contribuindo de maneira irreal para a previsão local.
Em contraste, um gráfico de Efeitos Locais Acumulados (ALE) irá dividir as instâncias em grupos semelhantes e forçar a variável de interesse apenas nesse intervalo de amostras, reduzindo o efeito das outras variáveis. Além disso, ele não trabalha com a média das previsões diretamente, mas sim com a diferença entre a previsão com a variável em um valor específico e a previsão com a variável em outro valor próximo ao ponto de interesse. Acumulando esses efeitos locais (diferenças), conseguimos ver a contribuição do crescimento da variável no resultado final.
Vantagens dos ALEs em relação aos PDPs
Velocidade: Os ALE plots são mais rápidos de calcular do que os PDPs, pois requerem menos previsões do modelo. Enquanto os ALEs tem complexidade linear, os PDPs tem complexidade quadrática.
Interpretabilidade: Os ALEs são mais fáceis de interpretar do que os PDPs, pois mostram diretamente a contribuição da variável de interesse para a previsão. O que poderia ser utilizado para gerar uma decomposição funcional como a soma da contribuição para cada variável preditora.
Robustez: Os ALEs são mais robustos do que os PDPs em relação a correlações entre as variáveis preditoras, pois pegando amostras semelhantes o efeito das outras variáveis é reduzido.
Interação de Variáveis: Além disso, os ALEs podem ser usados para visualizar interações entre variáveis. Caso plotemos o ALE de duas variáveis, o resultado será apenas a interação entre elas e não o efeito combinado das duas variáveis.
Decomposição Funcional: A soma do efeito local acumulado de todas as variáveis pode ser usada como uma aproximação do modelo, permitindo uma melhor compreensão de como o modelo funciona.
Implementando ALEs com Python
Passo 1: Preparação do Ambiente
# Instalando as bibliotecas necessárias
!pip install pandas numpy scikit-learn matplotlib xgboost PyALE
# Importando as bibliotecas necessárias
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import xgboost as xgb
from PyALE import ale
from sklearn.model_selection import train_test_splitPasso 2: Preparação dos Dados e Treinamento do Modelo
# Carregar os dados
arquivo = '/content/drive/MyDrive/Datasets Públicos/Battery_RUL.csv' # Endereço do arquivo .csv
df = pd.read_csv(arquivo)
# Separar features e target
X = df.drop('RUL', axis=1)
y = df['RUL']
# Dividir em treino e teste
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Criar e treinar um modelo (vamos usar XGBoost como exemplo)
model = xgb.XGBRegressor(n_estimators=500, random_state=42)
model.fit(X_train, y_train)Passo 3: Calculando o ALE 1D:
def calcular_ale_1d(modelo, X, coluna, grid_size=40):
ale_eff = ale(X=X, model=modelo, feature=[coluna],
grid_size=grid_size, include_CI=False,
plot=False)
return ale_eff
ale_eff = calcular_ale_1d(model, X_train, 'Max. Voltage Dischar. (V)')
ale_effEssa função retorna uma série com os efeitos ALE para a variável especificada. Você pode plotar os resultados trocando plot=False por plot=True utilizar a função abaixo:
def plotar_ale_1d(ale_eff, coluna, ax):
ax.plot(ale_eff.index, ale_eff['eff'])
ax.set_title(f'ALE para {coluna}')
ax.axhline(y=0, color='gray', linestyle='--')
ax.tick_params(axis='x', rotation=45)
ax.set_xlabel(coluna)
ax.set_ylabel('Efeito')
# Encontrar pontos de cruzamento onde a curva cruza y=0
indices = ale_eff['eff'].index
eff = ale_eff['eff'].values
cruzamentos = np.where(np.diff(np.sign(eff)))[0]
x_min, x_max = indices.min(), indices.max()
ax.set_xlim(x_min, x_max)
for cruzamento in cruzamentos:
x0, x1 = indices[cruzamento], indices[cruzamento + 1]
y0, y1 = eff[cruzamento], eff[cruzamento + 1]
cruzamento_x = x0 - y0 * (x1 - x0) / (y1 - y0)
ax.axvline(x=cruzamento_x, color='red', linestyle='--')
ax.set_xticks(np.append(ax.get_xticks(), cruzamento_x))
fig, ax = plt.subplots(figsize=(10, 6))
plotar_ale_1d(ale_eff, 'Max. Voltage Dischar. (V)', ax)
plt.show()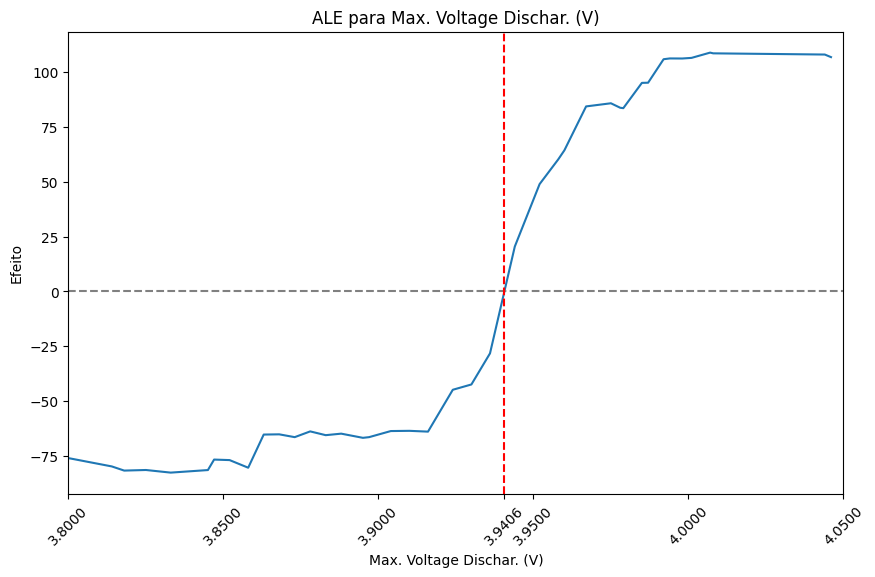
Passo 4: Calculando e Plotando o ALE 2D
def calcular_ale_2d(modelo, X, colunas, grid_size=40):
ale_eff_2d = ale(X=X, model=modelo, feature=colunas,
grid_size=grid_size, plot=False)
return ale_eff_2d
ale_eff_2d = calcular_ale_2d(model, X_train, ['Max. Voltage Dischar. (V)', 'Discharge Time (s)'])
ale_eff_2dAtenção: o ALE 2D calcula apenas o efeito da interação entre as duas variáveis, não incluindo os efeitos individuais de cada uma.
Da mesma forma, você pode plotar os resultados nativamente ou utilizar a função abaixo:
def plotar_ale_2d(ale_eff_2d, colunas, ax, titulo="ALE 2D (Interação)"):
im = ax.imshow(ale_eff_2d.values, interpolation='nearest', aspect='auto', origin='lower',
extent=[ale_eff_2d.columns[0], ale_eff_2d.columns[-1],
ale_eff_2d.index[0], ale_eff_2d.index[-1]])
ax.set_title(titulo)
ax.set_xlabel(colunas[1])
ax.set_ylabel(colunas[0])
plt.colorbar(im, ax=ax)
plt, ax = plt.subplots(figsize=(10, 6))
plotar_ale_2d(ale_eff_2d, ['Max. Voltage Dischar. (V)', 'Discharge Time (s)'], ax)
plt.show()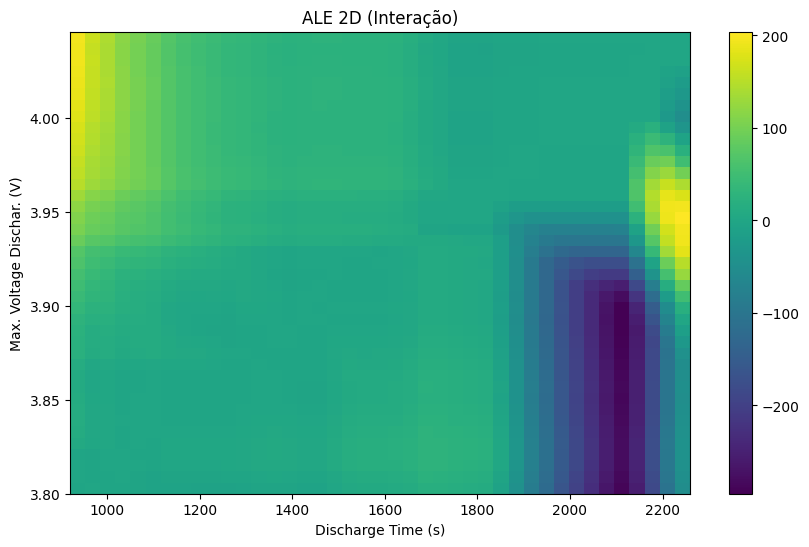
Passo 5: Combinando os Efeitos 1D e 2D
Caso sua intenção seja saber o efeito total da combinação das variáveis, você pode combinar os efeitos 1D e 2D. Para isso, utilize a função abaixo:
def combinar_ales(ales_1d, ale_2d):
ale_composto = ale_2d.copy()
for i in [0, 1]:
ale_composto = ale_composto.T
for local in ales_1d[i].index:
ale_composto[local] += ales_1d[i].loc[local]['eff']
return ale_composto
ale_effs = [ale_eff, calcular_ale_1d(model, X_train, 'Discharge Time (s)')]
ale_composto = combinar_ales(ale_effs, ale_eff_2d)
ale_compostoPara plotar o efeito composto, utilize a função plotar_ale_2d com o resultado da função acima.
plt, ax = plt.subplots(figsize=(10, 6))
plotar_ale_2d(ale_composto, ['Max. Voltage Dischar. (V)', 'Discharge Time (s)'], ax)
plt.show()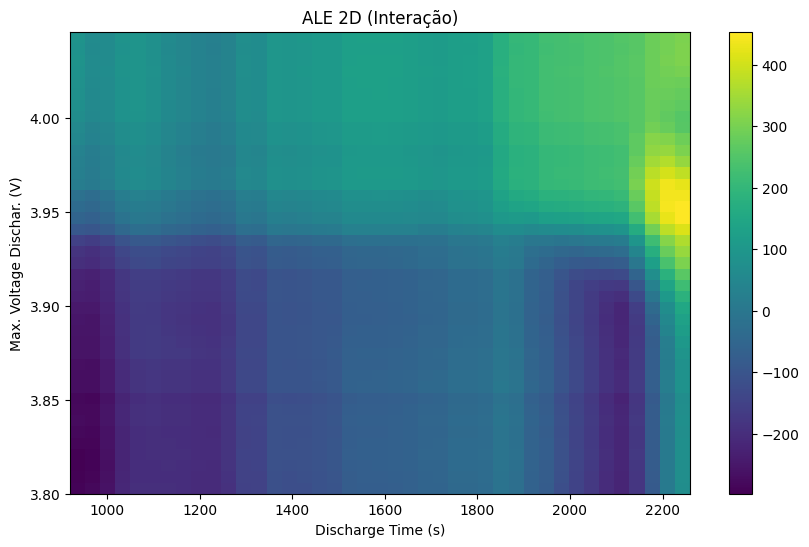
Passo 6: Função para Análise Completa
A função abaixo realiza a análise completa, calculando e plotando os efeitos ALE tanto em 1D quanto em 2D, além do efeito composto que combina os dois.
def realizar_analise_ale(modelo, X, colunas, grid_size=40):
fig, axs = plt.subplots(2, 2, figsize=(15, 15))
fig.suptitle('Análise dos Efeitos Locais Acumulados (ALE)')
axs = axs.flatten() # Transforma em array 1D para facilitar indexação
# Cálculo dos efeitos ALE 1D
ale_eff_1d_coluna1 = calcular_ale_1d(modelo, X, colunas[0], grid_size)
ale_eff_1d_coluna2 = calcular_ale_1d(modelo, X, colunas[1], grid_size)
# Plotagem do ALE 1D
plotar_ale_1d(ale_eff_1d_coluna1, colunas[0], axs[0])
plotar_ale_1d(ale_eff_1d_coluna2, colunas[1], axs[1])
# Cálculo do efeito ALE 2D e composto
ale_eff_2d = calcular_ale_2d(modelo, X, colunas, grid_size)
ale_composto = combinar_ales([ale_eff_1d_coluna1, ale_eff_1d_coluna2], ale_eff_2d)
# Plotagem do ALE 2D e composto
plotar_ale_2d(ale_eff_2d, colunas, axs[2], titulo="ALE 2D (Interação)")
plotar_ale_2d(ale_composto, colunas, axs[3], titulo="ALE Composto (2D + 1D)")
plt.tight_layout()
plt.show()
return ale_eff_1d_coluna1, ale_eff_1d_coluna2, ale_eff_2d, ale_composto
realizar_analise_ale(model, X_train, ['Max. Voltage Dischar. (V)', 'Discharge Time (s)'])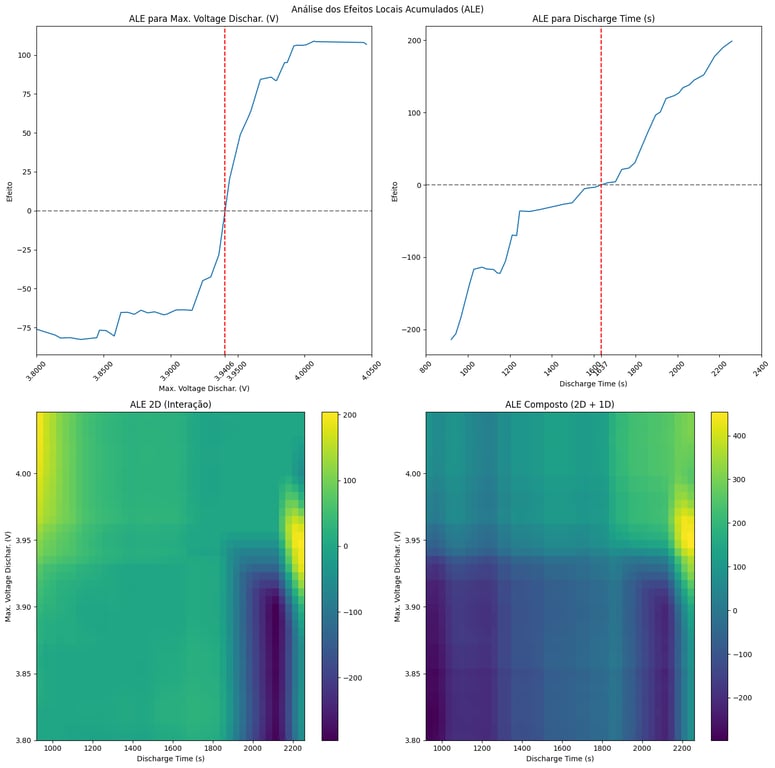
Conclusão
Os Accumulated Local Effects (ALEs) são uma técnica poderosa para interpretabilidade de modelos de machine learning. Eles oferecem vantagens significativas em relação aos tradicionais Partial Dependence Plots (PDPs), como a capacidade de capturar interações entre características e maior robustez.
Você pode experimentar este código no Google Colab. Faça uma cópia do notebook e adapte-o para seus próprios dados e necessidades. Se tiver alguma dúvida, você pode consultar a documentação oficial do PyALE ou entrar em contato comigo.