Gráficos de Dependência Parcial (PDP)

Os Partial Dependence Plots (PDP) são uma ferramenta excelente para interpretar modelos de machine learning. Eles nos ajudam a entender como uma característica específica influencia as previsões do modelo, mantendo todas as outras características constantes.

Por que PDPs são importantes na Manutenção Preditiva?

Na manutenção preditiva, frequentemente trabalhamos com modelos complexos que consideram múltiplas variáveis: temperatura, vibração, pressão, tempo de operação, etc. Embora esses modelos possam ter uma alta precisão, nem sempre é fácil entender como eles chegam às suas conclusões.

Por exemplo, imagine que temos um modelo que prevê a vida útil restante de um equipamento. Algumas perguntas importantes seriam:

Como a temperatura afeta a vida útil prevista?
Existe um ponto crítico de vibração que reduz drasticamente a vida útil?
A partir de quantas horas de operação o risco de falha aumenta significativamente?

Os PDPs nos ajudam a responder exatamente esse tipo de pergunta.

Intuição do Funcionamento:

Imagine que você é um técnico de manutenção experiente e quer explicar para um novato como a temperatura afeta a vida útil de uma máquina. Você poderia dizer:

Para entender o efeito da temperatura, vamos fazer um exercício mental: para cada temperatura possível, vamos imaginar que todas as máquinas estivessem operando nessa temperatura, mantendo suas outras características (vibração, pressão, etc.) exatamente como estão. Então, calculamos a média da vida útil prevista para cada temperatura.

É exatamente isso que um PDP faz para todos os valores possíveis da característica que queremos analisar.

Implementando PDPs com Python

Neste exemplo, vamos usar uma base de dados em formato .csv, que contém informações sobre uma bateria. Nosso objetivo é prever a vida útil restante da bateria com base nas variáveis disponíveis. Esse dataset pode ser encontrado no kaggle. Você pode baixar o arquivo aqui.

Passo 1: Preparação do Ambiente

# Instalando as bibliotecas necessárias
!pip install pandas numpy scikit-learn matplotlib

# Importando as bibliotecas necessárias
import pandas as pd
import numpy as np
import xgboost as xgb
from sklearn.model_selection import train_test_split
from sklearn.inspection import PartialDependenceDisplay
import matplotlib.pyplot as plt

Passo 2: Preparação dos Dados e Treinamento do Modelo

# Carregar os dados
arquivo = '/content/drive/MyDrive/Datasets Públicos/Battery_RUL.csv' # Endereço do arquivo .csv
df = pd.read_csv(arquivo)

# Separar features e target
X = df.drop('RUL', axis=1)
y = df['RUL']

# Dividir em treino e teste
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Criar e treinar um modelo (vamos usar XGBoost como exemplo)
model = xgb.XGBRegressor(n_estimators=500, random_state=42)
model.fit(X_train, y_train)

Passo 3: Criando os PDPs 1D

# Criar um PDP 1D para analisar a influência da 'Max. Voltage Dischar. (V)'
PartialDependenceDisplay.from_estimator(model, X_train , ['Max. Voltage Dischar. (V)'])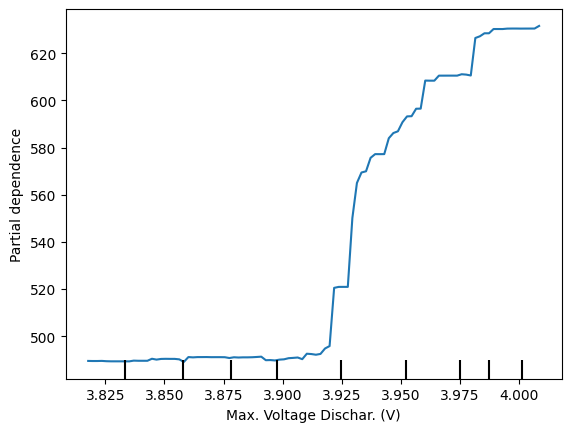

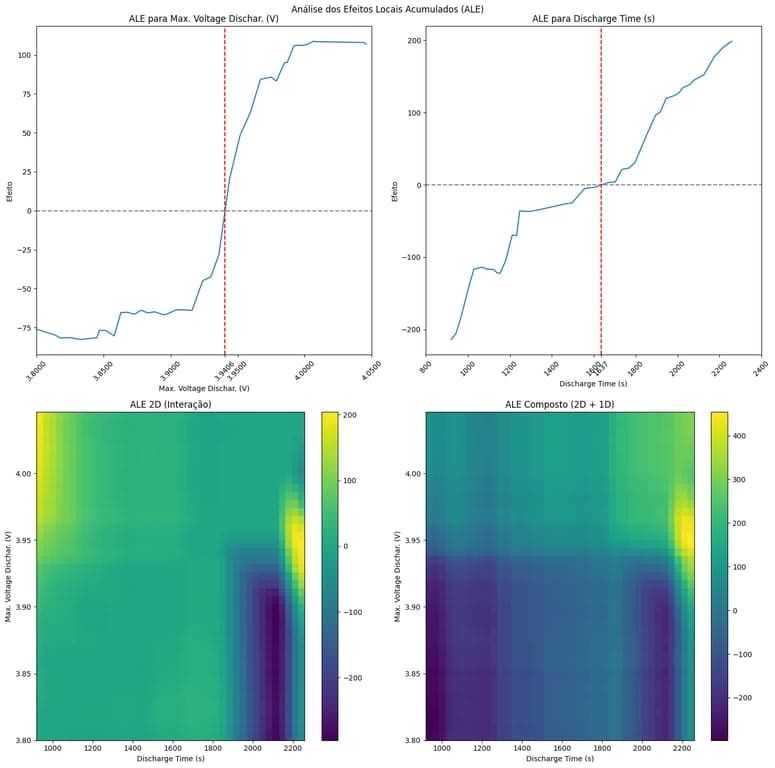
Podemos observar claramente na imagem acima uma divisão entre os valores com RUL mais baixo e mais alto (observe a separação que ocorre em torno de 3.925), esse insight pode ser crucial para identificar pontos críticos de falha.

Passo 4: Criando os PDPs 2D

# Criar um PDP 2D para analisar interações
def plotar_pdp_2d(modelo, x, colunas):
    fig, axs = plt.subplots(1, 3, figsize=(18, 6))
    for i, coluna in enumerate(colunas):
        PartialDependenceDisplay.from_estimator(modelo, x, [coluna], ax=axs[i])
                                          
    PartialDependenceDisplay.from_estimator(modelo, x, [tuple(colunas)], ax=axs[2])
    plt.show()

plotar_pdp_2d(model, X_train, ['Max. Voltage Dischar. (V)', 'Discharge Time (s)'])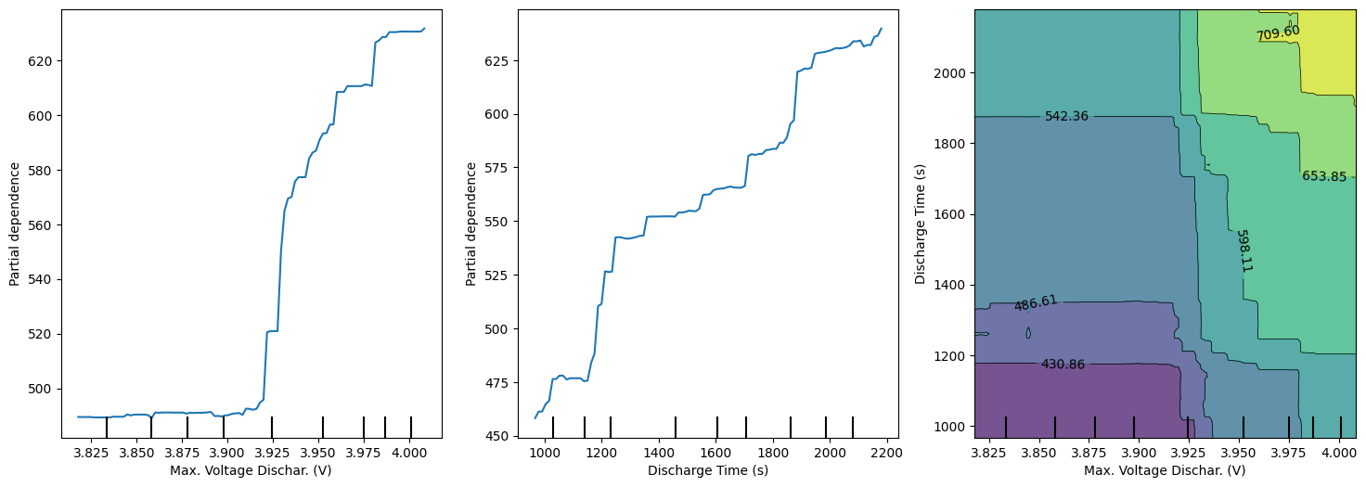

Através do PDP 2D, podemos observar como a interação entre as características 'Max. Voltage Dischar. (V)' e 'Discharge Time (s)' afeta a previsão do modelo. Permitindo uma análise mais aprofundada das relações entre as características.

Insights Extraídos dos PDPs

Ao analisar os PDPs gerados, podemos extrair insights valiosos:

1. Tipo de Relação: Os PDPs mostram claramente como o aumento ou diminuição de uma característica afeta a previsão. Através da curva gerada podemos identificar, por exemplo, se a relação é linear, exponencial, se existe um ponto de inflexão, etc.

2. Interações: Os PDPs 2D revelam como diferentes características interagem entre si, o que pode ser crucial para captar relações mais complexas.

Limitações dos PDPs

É importante mencionar algumas limitações:

1. Assumem Independência: PDPs assumem que as características são independentes, o que nem sempre é verdade na prática.

2. Média dos Efeitos: Por trabalhar com médias, podem mascarar efeitos importantes em subgrupos específicos ou ser sensíveis a outliers.

3. Custo Computacional: Para datasets muito grandes ou modelos complexos, o cálculo dos PDPs pode ser computacionalmente custoso.

Caso esteja enfrentando algum desses problemas, recomendo que leia o post sobre ALE (Accumulated Local Effects), que é uma alternativa mais robusta, eficiente e considera interações entre características.